- 回帰問題について、実例を用いながら説明
- 線型回帰・非線形回帰の簡単な数式と概要
- 回帰モデルのパラメータ推定方法(平均二乗誤差、最小二乗法)
この記事では、回帰モデルについての概要と、線形・非線形の違いについて説明します。
回帰問題とは
回帰問題
データの特徴量(説明変数)と目的変数との関係をモデリングし、特徴量から目的変数の値を予測する問題です。
回帰モデルは、連続値を持つ目的変数を予測する問題に使用される教師あり学習です。
ある入力(離散値あるいは連続値)が与えられたときの出力(連続値)を予測します。
実社会においては以下のようなケースで使用されます。
例1: 不動産価格の予測
- 問題: 各独立変数の影響を考慮して、新しい物件の不動産価格を予測したい。
- 説明変数: 家の面積、築年数、部屋数、立地(地域)、近隣の学校の質など。
- 目的変数: 家の販売価格。
例2: 広告支出と売上の関係分析
- 問題: 広告支出が売上にどのような影響を与えるかを知りたい。
- 説明変数: 異なるメディア(テレビ、ラジオ、インターネット)に対する広告支出。
- 目的変数: 売上高。
例3: 気象データを使用した作物の収穫予測
- 問題: 天候変化に基づいて作物の収量を予測したい。
- 説明変数: 降水量、温度、日照時間など。
- 目的変数: 作物の収量。
線形回帰と非線形回帰
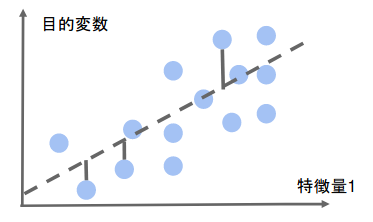
下図のように直線を引いて予測する場合を「線型回帰」、曲線を引いて予測する場合を「非線形回帰」と呼びます。
線型回帰
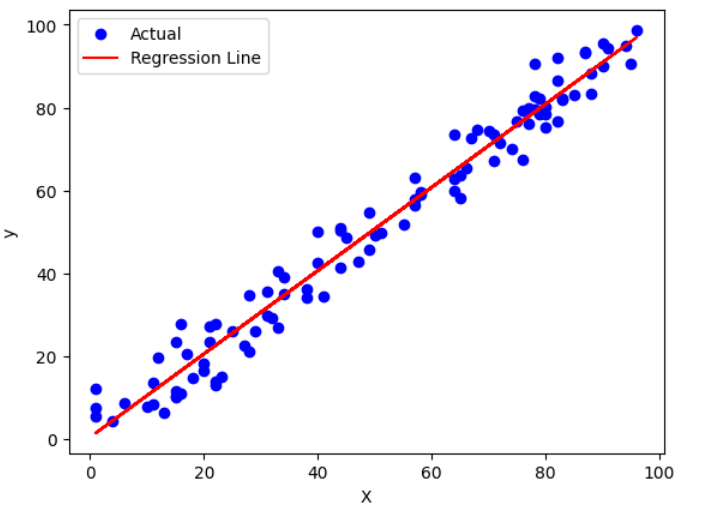
直線で予測する
非線型回帰
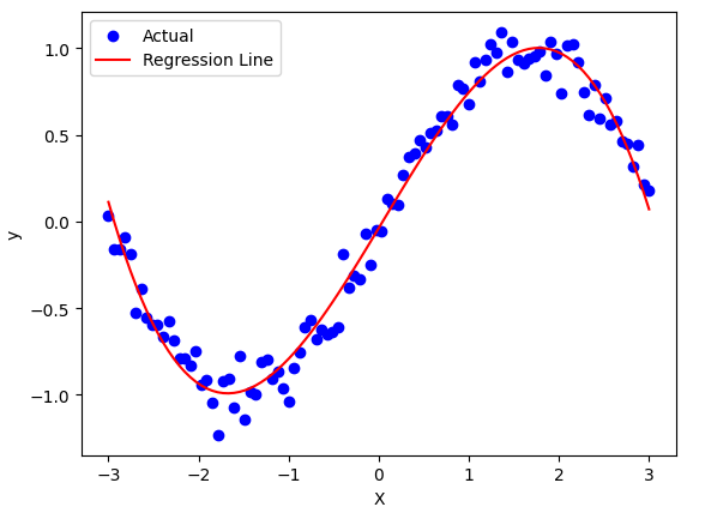
曲線で予測する
線型回帰(Linear Regression)
線型回帰は説明変数が1次元の場合に「単回帰」、多次元の場合に「重回帰」と呼びます。
以下に単回帰と重回帰それぞれの数式を示します。
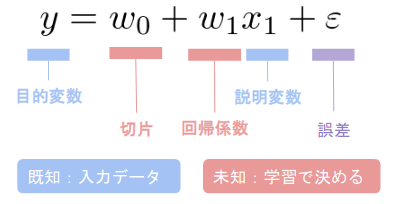
既知の入力データを用いて学習し、切片と回帰係数を求めます。
また、データは回帰直線に誤差が加わり観測されていると仮定します。
単回帰
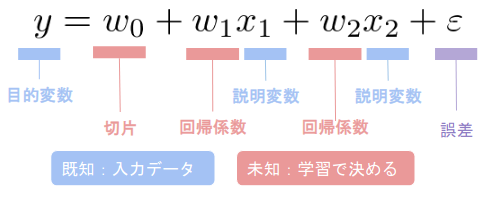
重回帰
非線型回帰(Nonlinear regression)
非線形回帰はデータが線形モデルでは適切に説明できない場合や、より複雑な関係性を探求する必要がある場合に、重要なツールとなります。
ただし、モデルの複雑さと過学習のリスクを考慮する必要があります。
非線形回帰モデルは次の形式をとります。
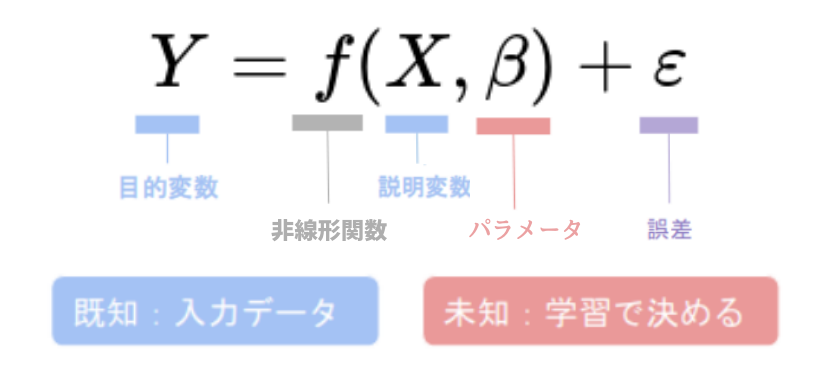
非線形回帰ではデータに非線形性を導入するために、Xと β の関係を定義した非線形関数f(X)が使用されます。
これは、多項式、指数関数、対数関数、三角関数など、さまざまな形をとることができます。
- 指数関数: $$ f(X,β)=β_0\exp(β_1 X) $$
- 対数関数: $$ f(X,β)=β_0 + β_1\log(X) $$
- 三角関数: $$ f(X,β)=β_0 + β_1\sin(X) + β_2\cos(X) $$
回帰モデルのパラメータ推定
平均二乗誤差(Mean Squared Error, MSE)
平均二乗誤差(MSE)は、回帰モデルの予測値と実測値の間の誤差(残差)を評価する指標です。
MSEは、各データポイントにおける残差の二乗を平均した値で、以下の数式で表されます。
$$ MSE = \frac{1}{n} \sum_{i}^{n} (y_i – y_i^{pred})^{2} $$
nはデータ数、yは実測値、y_predは回帰モデルによる予測値です。
MSEは残差の二乗の平均を取るため、予測値と実測値の差の大きさを考慮し、誤差の大きさを表します。
MSEが小さいほど予測が実測値に近いことを示します。
最小二乗法(Ordinary Least Squares, OLS)
最小二乗法は、回帰モデルのパラメータ(回帰係数)を推定するための手法です。
学習データの平均二乗誤差を最小化するようにパラメータを模索します。
最小化は、勾配が0になる点を求めれば良いです。
最小二乗法によって求められた回帰係数を用いて予測を行い、その予測値と実測値の間の誤差をMSEで評価することが一般的です。
最小二乗法に基づく回帰モデルは、MSEを最小化することを目指しており、MSEが小さいほどモデルの予測性能が高いことを示します。
最小二乗法は、線形回帰モデルにおいて広く使用される手法ですが、非線形な回帰モデルや他のタイプのモデルでは別の最適化手法が必要になる場合もあります。
また、最小二乗法は誤差の二乗和を最小化するため、外れ値などの大きな誤差に敏感になる傾向があります。
そのため、データに外れ値が含まれる場合や誤差の分布が非対称な場合には、最小二乗法による回帰モデルが適切ではないことがあります。
続いて、pythonコードを用いて実装していきましょう。
線形回帰分析はこちら↓
非線形回帰分析はこちら↓