- python×scikit-learnでの単回帰分析の実装コード
- 単回帰分析の評価方法
import pandas as pd
import numpy as np
# 説明変数(特徴量)の作成
data = pd.DataFrame({
'X': np.random.randint(0, 100, size=100)
})
# 目的変数の作成
data['y'] = data['X'] + np.random.normal(0, 5, size=100)
X = data[['X']]
y = data['y']
plt.scatter(X, y, color='blue', label='Actual')
plt.show()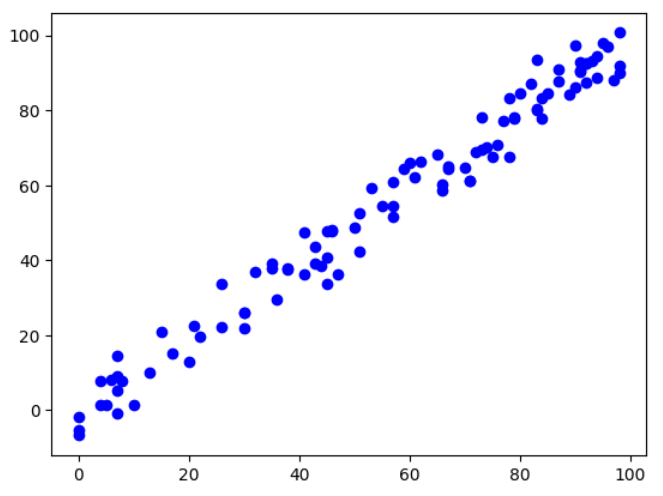
本記事では、このデータに対して単回帰モデルの作成と評価をしていきます。
目次
単回帰分析の実装コード
今回の実装コードです。
詳細について解説していきます。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# 説明変数(特徴量)の作成
data = pd.DataFrame({
'X': np.random.randint(0, 100, size=100) # 説明変数(特徴量)
})
# 目的変数の作成
data['y'] = data['X'] + np.random.normal(0, 5, size=100)
# 説明変数と目的変数の分割
X = data[['X']]
y = data['y']
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 0.3, random_state = 666)
# LinearRegressionモデルの作成とトレーニング
model = LinearRegression()
model.fit(X_train, y_train)
# 回帰直線の描画
plt.scatter(X, y, color='blue', label='Actual')
plt.plot(X_train, model.predict(X_train), color='red', label='Regression Line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
# 作成したモデルから予測(学習用、検証用モデル使用)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# 単回帰の回帰係数と切片を出力
print('回帰係数: %.3f, 切片 : %.3f' % (model.coef_, model.intercept_))
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))
# 学習用、検証用それぞれで残差をプロット
plt.scatter(y_train_pred, y_train_pred - y_train, marker = 'o', label = 'Train Data')
plt.scatter(y_test_pred, y_test_pred - y_test, marker = 's', label = 'Test Data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.legend(loc = 'upper left')
# y = 0に直線を引く
plt.hlines(y = 0, xmin = -10, xmax = 110, lw = 2, color = 'red')
plt.xlim([0, 100])
plt.show()データ準備とモデル作成
データの分割
# 70%を学習用、30%を検証用データにするよう分割
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size = 0.3, random_state = 666)ホールドアウト法で分割を行っています。
学習
# LinearRegressionモデルの作成とトレーニング
model = LinearRegression()
model.fit(X_train, y_train)LinearRegression()に設定できる引数は以下の通り色々ありますが、今回はなにも設定してません。
- fit_intercept : bool, default=True
切片(y切片)をモデルに含めるかどうかを指定します。 - normalize : bool, default=False
特徴量の正規化を行うかどうかを指定します。 - copy_X : bool, default=True
特徴量行列のコピーを作成するかどうかを指定します。 - n_jobs : int or None, default=None
計算に使用するジョブの数を指定します。intの場合、指定した数のジョブが使用されます。
結果の可視化
回帰直線
# 回帰直線の描画
plt.scatter(X, y, color='blue', label='Actual')
plt.plot(X_train, model.predict(X_train), color='red', label='Regression Line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()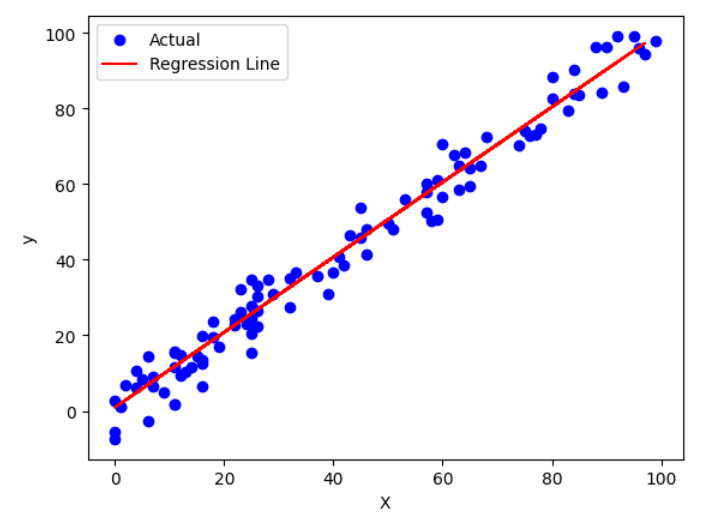
回帰係数と切片
# 単回帰の回帰係数と切片を出力
print('回帰係数: %.3f, 切片 : %.3f' % (model.coef_, model.intercept_))回帰係数: 1.007, 切片 : -0.662
単回帰モデルの性能評価
単回帰分析の評価指標として、代表的なのは以下の3つがあります。
- 平均二乗誤差(Mean Squared Error, MSE)
- 決定係数
- 残差
平均二乗誤差(Mean Squared Error, MSE)
# 学習用、検証用データに関して平均二乗誤差を出力
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))MSE Train : 34.994, Test : 33.334
平均二乗誤差は予測値と実測値の差の二乗の平均です。
MSEは予測値と実測値のズレの大きさを表し、値が小さいほど良いモデルと言えます。
決定係数R2(Coefficient of Determination, R-squared)を用いた性能評価
# 学習用、検証用データに関してR^2を出力
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))R^2 Train : 0.961, Test : 0.968
決定係数はモデルが観測データをどれくらい説明できるかを示す指標です。
予測値の分散を実測値の分散で割った値で表され、0から1の範囲の値を取ります。
決定係数が1に近いほどモデルが良くデータを説明できていることを意味します。
残差(Residual)
# 学習用、検証用それぞれで残差をプロット
plt.scatter(y_train_pred, y_train_pred - y_train, marker = 'o', label = 'Train Data')
plt.scatter(y_test_pred, y_test_pred - y_test, marker = 's', label = 'Test Data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.legend(loc = 'upper left')
# y = 0に直線を引く
plt.hlines(y = 0, xmin = -10, xmax = 110, lw = 2, color = 'red')
plt.xlim([0, 100])
plt.show()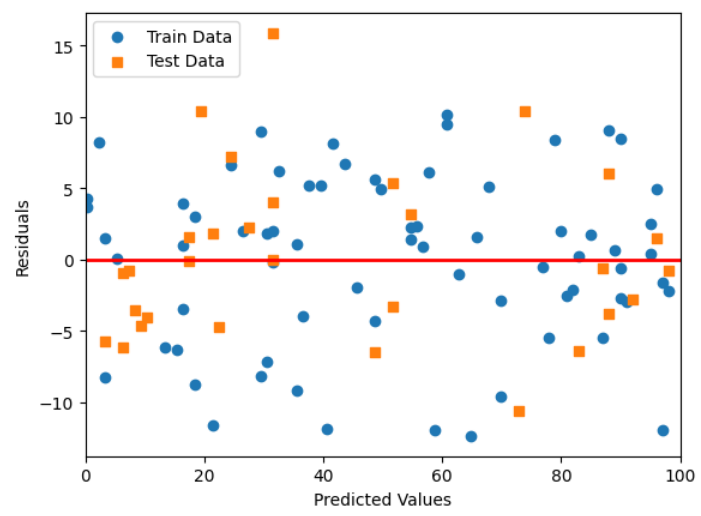
残差とは、観測された実際のデータ値とモデルによって予測された値との差のことです。
大きな残差は、モデルがそのデータポイントを適切に予測できていないことを示しています。
残差のパターン(例えば、系統的な傾向や非ランダム性)を分析することで、モデルの改善に繋がることがあります。
これらの指標は、単回帰分析において予測モデルの性能を評価する際に使用されます。
具体的な評価指標の計算方法は、予測値と実測値の対応するデータ点の集合を用意し、それを元に指標を計算することで求めることができます。
ただし、評価指標は問題の性質や目的に応じて選択する必要があります。
適切な評価指標を選択するためには、問題の背景や要件を考慮し、適切な指標を選ぶことが重要です。