機械学習で使う線形代数学の基本について、初学者向けに整理しました。
- 線形代数学の基本用語
- 固有値・固有ベクトルや固有値分解・特異値分解の概要と計算方法
線形代数学の基本用語
・スカラー
「+」「-」「×」「÷」ができてベクトルに対する係数になれる、単なる数値の値のことです。
例えば1,5,100など、よく使用している数値をスカラーと呼びます。
・ベクトル
数値の並びを表します。
ベクトルは大きさと向きを持ち、矢印で表示されます。
\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}
・行列 \( A \)
スカラーを表にし、ベクトルを並べたものになります。
画像処理でよく使われる形式です。
$$ A=\begin{bmatrix} a & b \\ c & d \end{bmatrix} $$
a,b,c,dには適当なスカラーが入る。
・行列式
1つの正方行列に対応する大きさみたいなもので、2行2列の場合は以下の式で表されます。
行列式が正であれば、その行列は向きを保った空間を拡大する行列であり、負であれば向きを反転させる行列となります。
$$ \begin{bmatrix} a & b \\ c & d \end{bmatrix} = ad – bc $$
・単位行列 \( I \)
かけてもかけられても変化しない行列のことです。
すべての対角成分が1でそれ以外の成分が0の正方行列になります。
$$ I=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $$
・逆行列 \( A^{-1} \)
ある正方行列Aに対して、Aとの積が単位行列Iとなるような行列で逆数のような働きをします。
$$ AA^{-1} = A^{-1}A = I $$
2行2列の場合は以下の通り求めることができます。
$$ A^{-1} = \frac{1}{ad – bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} $$
逆行列を求めることで線形方程式(未知数が1次式の方程式)を解いたり、行列を除算することができます。
注意点としては、逆行列が存在するためには正則行列(行列式が0でない行列)である必要があります。
固有値と固有ベクトル
行列Aに対して、スカラーλと0でないベクトル\(\vec{x}\)が存在して以下の式が成立する場合、
λをAの固有値、\(\vec{x}\)をAの固有ベクトルと呼びます。。
$$ A\vec{x} = λ\vec{a} $$
固有ベクトルは行列Aをかけると、ベクトルの方向が変わらずにスカラー倍される性質を持ち、行列がどのような変換を行っても方向が変わらない特別な方向ベクトルです。
また、固有値はその行列の変換がどの程度ベクトルを拡大、縮小するかを示すスカラー値になります。
固有値・固有ベクトルは機械学習、画像処理や音声処理で用いられています。
\(A=\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)の場合、以下の通りもとめることができます。
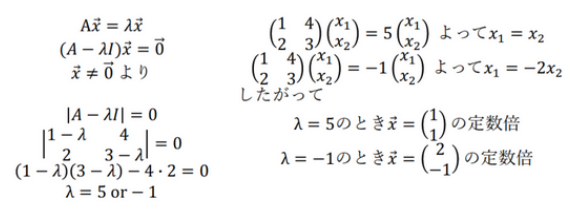
固有値分解
固有値分解とは正方行列Aを対角化する手法の1つで、固有値と固有ベクトルを用いてAを以下のように分解することを指します。
$$ A = V\Lambda V^{-1} $$
Vは固有ベクトルを列ベクトルとして並べた正方行列、Λは対角成分に固有値を持つ対角行列を示す。
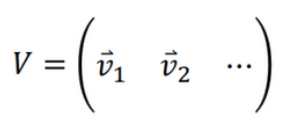
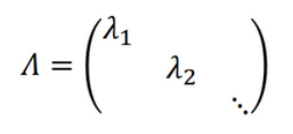
固有値分解によってAは固有ベクトルを新しい座標軸とする変換行列Vで対角化され、対角成分の要素が固有値になります。
行列を固有ベクトルで表現することで以下のような利点が得られます。
- データの重要な情報を抽出
⇨主成分分析や特異値分解など、データ圧縮や次元削減に用いられる。 - 行列の累乗を効率的に計算
⇨行列のn乗を計算する場合、固有値のn乗を計算するだけで元の行列を高速に計算できる。
\(A=\begin{bmatrix} 2 & 1 \\ 0 & 6 \end{bmatrix} \)とした場合、求め方の以下の通りです。
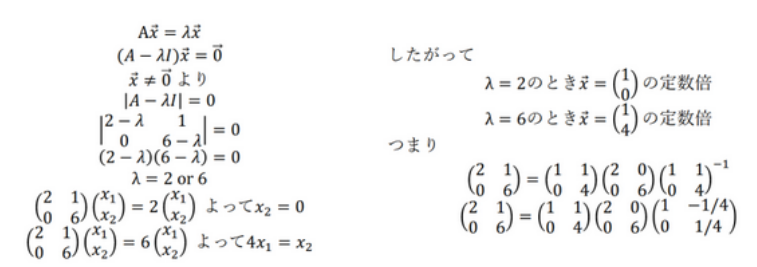
特異値分解(Singular Value Decomposition:SVD)
固有値分解は正方行列に対して行われる分解であるのに対し、特異値分解は任意の形の行列に対して行うことができます。
特異値分解は実数が⻑方形にならんだ行列Mを以下のように分解することです。
$$ M = USV^{-1} $$
行列M に対して、以下のような式が成り立つような特殊な単位ベクトル\(\vec{v}\),\(\vec{u}\) と右辺の係数σがあるとき、
$$ M\vec{v} = σ\vec{u} $$
$$ M^T\vec{u} = σ\vec{v} $$
単位ベクトル(\vec{v}\)を行列M に対する右特異ベクトル、\(\vec{u}\) を左特異ベクトル、係数σを特異値と呼びます。
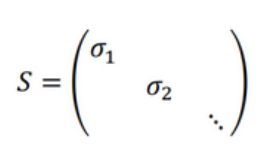
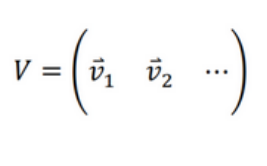
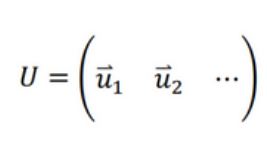
上記のような特異値を対角線上に並べた行列S(それ以外の成分は0)と、これに対応する特異ベクトルを並べた行列V、Uがあるとき、これらは以下のように関係付けることができます。
$$ MV = US $$
$$ M^TU = VS^T $$
$$ M = USV^{-1} $$
$$ M^T = VS^TU^{-1} $$
これらの積を掛け合わせると、以下のように変形できます。
$$ MM^T = USV^{-1} VS^TU^{-1} = USS^TU^{-1} $$
したがって、\(MM^T\) を固有値分解すれば,その左特異ベクトルUと特異値の 2 乗が求められます。
同様に、\(M^TM\) を固有値分解すれば,その右特異ベクトルVと特異値の 2 乗が算出されます。
このように\(MM^T\) と\(M^TM\) の固有値分解ができれば、行列Mの特異値分解が計算できます。
\(M =\begin{bmatrix} 1 & 2 &3 \\ 3 & 2 & 1 \end{bmatrix} \)とした場合、求め方の以下の通りです。
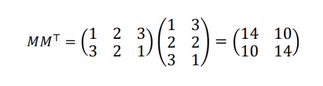

特異値は24,4,0の平方根をとり、\(12\sqrt{6}\), \(2\), \(0\)となります。
\(12\sqrt{6}\)に属する左特異ベクトルと右特異ベクトルはそれぞれ
$$ \frac{ 1 }{ \sqrt{2} }\begin{bmatrix} 1 \\ 1 \end{bmatrix} $$
$$ \frac{ 1 }{ \sqrt{3} }\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} $$
\(2\)に属する左特異ベクトルと右特異ベクトルはそれぞれ
$$ \frac{ 1 }{ \sqrt{2} }\begin{bmatrix} -1 \\ 1 \end{bmatrix} $$
$$ \frac{ 1 }{ \sqrt{2} }\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} $$
\(0\)に属する左特異ベクトルと右特異ベクトルはそれぞれ
$$ \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$$ \frac{ 1 }{ \sqrt{6} }\begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix} $$
として求められます。
以下に代表的な用途について記載します。
- データ圧縮
⇨低ランク行列として近似することができるため、画像などのデータ圧縮 - ノイズ除去
⇨ノイズの混入したデータを元の信号に近似
音声や画像処理においては、クリアな音声や画像に - 次元削減
⇨多次元のデータを低次元空間に写像
画像認識では画像を低次元空間に写像し、画像認識の精度向上が可能 - 推薦システム
⇨ユーザーの好みや嗜好に基づいてアイテムを推薦
映画の評価データを分解してユーザーの好みを把握し、おすすめの映画を提案 - 自然言語処理
⇨単語の意味をベクトル空間上で表現
文書中の単語を分解することで、単語の類似性や関連性を計算可能 - 画像認識
⇨画像の特徴量を抽出
輪郭やエッジを抽出するために分解し、特定の特異値に基づいて特徴量を抽出 - 数値解析
⇨数値解析において、行列方程式の解を求める
線形回帰分析や主成分分析などの手法で、行列方程式を解く
このように、特異値分解は画像処理、データ解析、自然言語処理、信号処理などの様々な分野に幅広く利用されている手法です。
少しイメージは湧きにくいですが、機械学習にとっては非常に大切です。

