- 確率やベイズ則の概要について
- 確率分布の種類(離散・連続)やその描画コード
機械学習で使う確率について、初学者向けに整理しました。
確率
確率とは、ある事象が起こる可能性の大きさを数値化したもので、主に2つの種類があります。
- 頻度確率(客観確率)
ある事象が観測された回数を全体の試行回数で割ったもの
例 10回のコイントスのうち表が6回出た場合、表が出る確率は 6/10 = 0.6 =60% - ベイズ確率(主観確率)
自分が持っている情報や経験から、ある事象が起こる確率を判断するもの
例 医者が患者に対して述べた確率「あなたの風邪の確率は40%です」
確率論は、統計学や情報理論、機械学習などの分野で広く応用され、自然現象の解明から、ビジネス戦略の立案まで、様々な問題解決に役立っています。
条件付き確率
条件付き確率とは「ある事象Bが起こる条件の下で、ある事象Aが起こる確率」のことです。
数式で表すとP(A|B)と表し、以下の式で計算できます( | は「~の条件の下で」という意味)
$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$
例えば、雪が降っている条件下で交通事故にあう確率などのことです。
通常の条件下より、交通事故に合う確率は高くなりそうですね。
独立な事象の同時確率
独立な事象の同時確率とは、お互いの発生に因果関係のない事象A,Bが同時に発生する場合の確率のことで、以下の式が成り立ちます。
$$ P(A \cap B) = P(A)P(B) = P(B)P(A) $$
ベイズ則
「ベイズ統計」と呼ばれる統計手法の一つで、事前に得られた情報をもとに、事後確率を更新する手法を指します。
ベイズの定理は以下の式で表されます。
$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$
この式から、以下3つのデータからP(A|B)を求めることができます。
P(B|A):「Aが与えられたときにBが起こる確率」
P(A):「Aが起こる確率」
P(B):「Bが起こる確率」
つまり、Bが起こったというデータから、Aが起こる確率を更新することができます。
このように、事前に得られた情報をもとに確率を更新する手法をベイズ統計と呼び、機械学習やデータ解析などの分野でよく使われています。
確率変数と確率分布
確率変数
確率変数とは、「ある事象と結び付けられた数値」のことであり、事象そのものを指す場合も多いです。
サイコロを投げる実験を考えた場合、確率変数Xを「サイコロの目」と定義することができます。
確率分布
確率分布とは、「確率変数がとりうる値とその値が出現する確率の関係」を表したものです。
確率変数Xを「サイコロの目」と定義した場合、確率分布は、Xが1から6の値をとる確率が1/6であるという情報を表したものとなります。
確率分布は離散的な場合と連続的な場合があり、離散的な場合は表やヒストグラムで表すことできます。
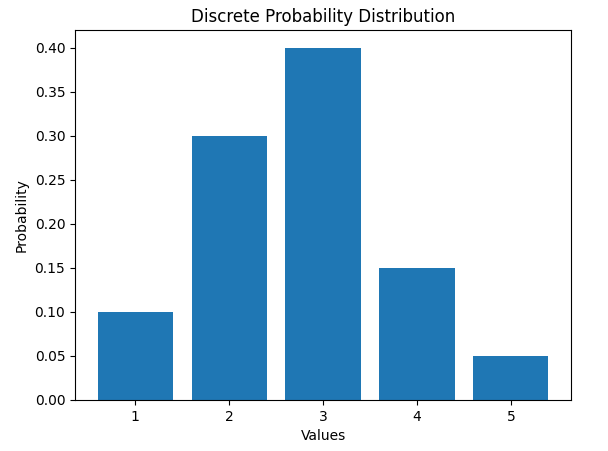
import matplotlib.pyplot as plt
import numpy as np
# 離散的な確率分布を作成
values = np.array([1, 2, 3, 4, 5])
probabilities = np.array([0.1, 0.3, 0.4, 0.15, 0.05])
# 確率が合計で1になるように正規化
probabilities = probabilities / probabilities.sum()
# 分布をプロット
plt.bar(values, probabilities)
plt.title("Discrete Probability Distribution")
plt.xlabel("Values")
plt.ylabel("Probability")
plt.xticks(values)
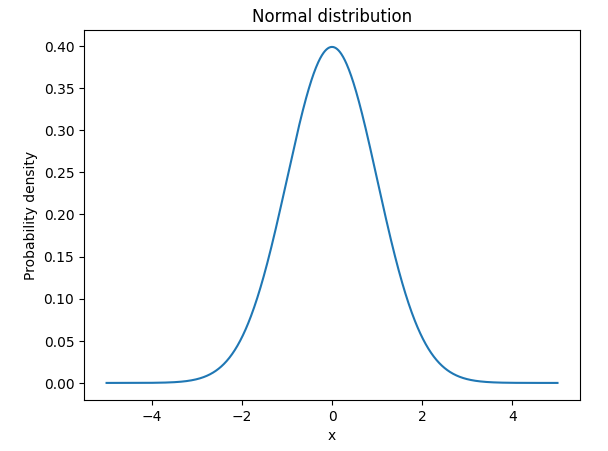
plt.show()一方で、確率変数が連続的な値を取るとき、確率は正規分布のような連続関数で考えることができます。
このときの関数を「確率密度関数」と呼びます。
正規分布の確率密度関数を描画すると、以下のように表せます。
import numpy as np
import matplotlib.pyplot as plt
# x軸の範囲を設定
x = np.linspace(-5, 5, 1000)
# 平均0, 標準偏差1の正規分布の確率密度関数を計算
pdf = 1/np.sqrt(2*np.pi) * np.exp(-0.5*x**2)
# グラフを描画
plt.plot(x, pdf)
plt.xlabel('x')
plt.ylabel('Probability density')
plt.title('Normal distribution')
plt.show()

