- 自己情報量・シャノンエントロピーの定義
- KLダイバージェンス・交差エントロピーの概要
自己情報量(Self-information)
自己情報量とはある出来事の予想されなさ(どれだけ意外なことか)を表す指標です。
自己情報量Iはその出来事が発生したときの情報量の減少量を表し、以下の式で定義されます。
$$ I(x) = – \log(P(x)) $$
ここでP(x)はその出来事が起こる確率を表します。
つまり、確率が低いほど自己情報量は大きくなり、確率が高いほど自己情報量は小さくなります。
例えば、コイントスで表が出るという出来事の自己情報量は確率が1/2であるため、
$$ I = -\log{_2}\frac{1}{2} = 1ビット $$
となります。
一方で、頻繁に発生する出来事の自己情報量は確率が高いため小さくなります。
自己情報量をpythonで描画してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 確率分布の定義
x = np.linspace(0.001, 1, 1000)
p = - np.log(x)
# プロット
plt.plot(x, p)
plt.xlabel('Probability')
plt.ylabel('Self-information')
plt.show()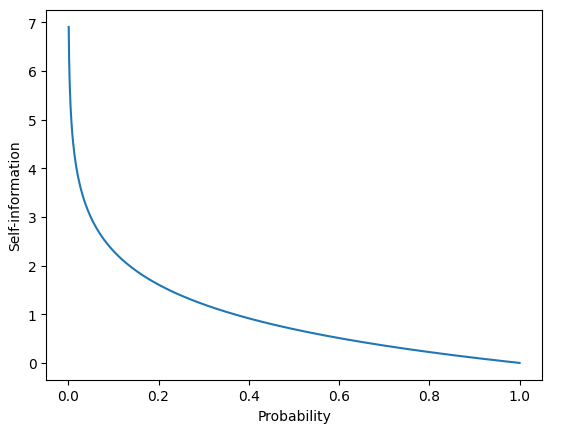
確率が0に近づくにつれて自己情報量が無限大になり、
確率が1に近づくと自己情報量が0になることがわかります。
自己情報量は予測モデルの評価に利用されます。
例えば、ある事象に対して予測を行って実際にその事象が発生した場合、
自己情報量を計算することで、予測の正確さを評価することができます。
他にも情報圧縮やデータ圧縮などの技術にも利用され、データの冗長性を減らすために用いられます。
自己情報量は情報理論において重要な概念の一つであり、確率論や統計学、機械学習などの分野で広く利用されています。
シャノンエントロピー
シャノンエントロピーとは、ある確率分布に基づく自己情報量の期待値を表します。
情報の不確実性の度合いを測る指標として広く利用されています。
確率変数XのシャノンエントロピーH(X)は確率p(x)を用いて以下の式で表されます。
$$ H(x) = E(I(x)) = -E(\log(P(x))) = -\displaystyle \sum_{}^{} (P(x)\log(P(x)))\ $$
確率的に起こりうる事象の情報量が小さいほどシャノンエントロピーは小さくなり、情報量が大きいほど、シャノンエントロピーは大きくなります。
この式は確率変数Xが取りうる値の種類が有限個の場合に適用されます。
コイントスのように表と裏が出る確率が1/2の場合、シャノンエントロピーは以下のように計算できます。
$$ H(x) = -(\frac{1}{2} \log{_2}\frac{1}{2} + \frac{1}{2} \log{_2}\frac{1}{2} ) = 1ビット $$
シャノンエントロピーは情報圧縮や通信の信号処理において、データの圧縮率や伝送効率を最大化するための理論的枠組みとして応用されます。
最後にpythonで描画してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# 確率分布の定義
x = np.linspace(0.001, 1, 1000)
p = np.vstack((x, 1-x))
# シャノンエントロピーの計算
H = -np.sum(p * np.log(p), axis=0)
# プロット
plt.plot(x, H)
plt.xlabel('Probability')
plt.ylabel('Shannon entropy')
plt.show()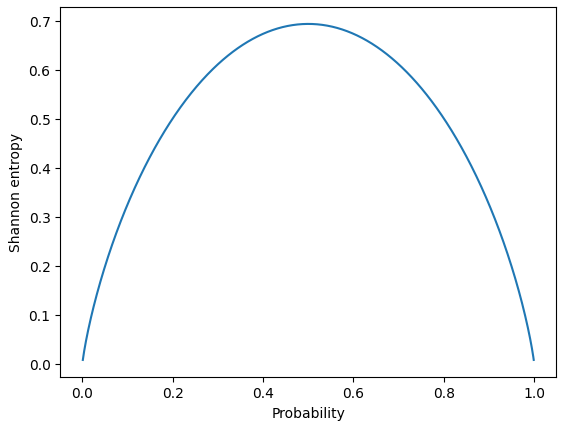
確率が等確率分布(0.5, 0.5)のとき、シャノンエントロピーが最大値であり、
確率が0または1に近づくにつれて、シャノンエントロピーが小さくなることがわかります。
カルバック・ライブラー(KL) ダイバージェンス
KLダイバージェンスは同じ事象・確率変数における2つの確率分布PとQの違いを表します。
KLダイバージェンスD(P||Q)は以下のように定義されます。
$$ D(P||Q) = \displaystyle \sum_{x}^{} P(x) \log \frac{P(x)}{Q(x)} $$
この式は確率分布Pの各要素xについて、P(x)をQ(x)で近似するために必要な情報量の差を求めて、それを全要素について足し合わせたものです。
KLダイバージェンスは非負であり、PとQが完全に等しい場合にのみ0になります。
したがって、KLダイバージェンスは2つの確率分布がどの程度異なるかを測る指標となります。
注意点として、KLダイバージェンスは非対称な指標ということです。
つまり、D(P||Q) ≠ D(Q||P)であることが一般に成り立ちます。
交差エントロピー(Cross Entropy)
交差エントロピーは、KLダイバージェンスの一部分を取り出したもので、2つの確率分布間の距離を測る指標の1つです。
2つの確率分布PとQが与えられたとき、交差エントロピーはQについての自己情報量をPの分布で平均します。
Pが正解ラベルの確率分布、Qが予測ラベルの確率分布であるとき、交差エントロピーH(P, Q)は以下のように定義されます。
$$ H(P, Q) = -\displaystyle \sum_{x}^{} P(x) \log Q(x) $$
この式は正解ラベルの各要素xについて、予測ラベルQ(x)がどの程度正解ラベルP(x)を近似できるかを示しています。
予測ラベルQ(x)が1に近づくほど、正解ラベルP(x)の情報量が減少し、H(P, Q)は小さくなります。
一方で、予測ラベルQ(x)が0に近づくほど、正解ラベルP(x)の情報量が増加し、H(P, Q)は大きくなります。
交差エントロピーは最小化したい損失関数としてよく使われます。
例えば、分類問題では正解ラベルと予測ラベルの間の交差エントロピーを損失関数として設定し、その損失を最小化するようにモデルを学習させます。


